My Wiki: Complex Base Numbers

Here are a few ideas about numbers and bases. This is not a new invention: http://en.wikipedia.org/wiki/Complex_base_systems

partnumbers and other ideas

Numbers are normally written on a number line

 ---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+
    0   1   2   3   4   5   6   7   8   9   10  11  12  13  14  15  16  ...  Decimal
    0   1   10  11  100 101 110 111 .... Binary

At lunch Barry asked something like can you have complex bases.

Example: Complex Number Lines for angles 120 degrees for Base 1.3333333333333

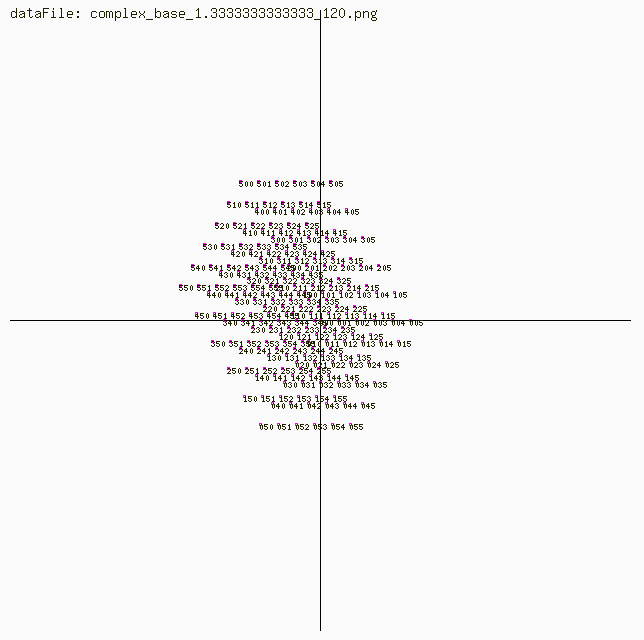
These were produced using: http://www.dougrice.plus.com/images/complex.lua

When you read a number like 123 you know that it means one hundred + twenty+ three units.

What happens if you replace the unit by a complex number?

We write down 123 as three symbols '1' , '2' , '3', from the ordered list 0,1,2,3,4,5,6,7,8,9,...

'1' means the value of 1.

so '1' = '0'+1, 2='1'+1, 3='2'+1, '0' has the value 0, '1' has the value 1 etc where the symbol to the right is +1, and to the left is -1

You can write down a number like 123 as 1 * 100 + 2 * 10 + 3

To convert it to an integer you can use a formula like:

  0123  = ( ( ( '0' )*10 + '1' )*10 + '2' )*10 + '3'

  where '0'..'9' evaluate to 0..1

What happens if you replace the unit with a complex number?

  0123  = ( ( ( '0' )*10 + '1'*CM )*10 + '2'*CM )*10 + '3'*CM

  I think it is just 123 * CM =  100*CM + 20*CM + 3*CM = 123*CM;

What happens if you replace the base '10' with a complex number represented by CM = (Re + j Im).

  0123  = ( ( ( '0' )*CM + '1' )*CM + '2' )*CM + '3'

  This needs a diagram

What happens if you replace the base '10' with a decimal like 0.1?

  Take 0123 and raise to 0.1

  0123  becomes 3.210 as  ( ( ( '0' )*0.1 + '1' )*0.1 + '2' )*0.1 + '3' = 3.210

  so 0123 becomes 0.01 + 0.2 + 3 = 3.210

You can with interesting results.

We have have vulgar numbers, like 0,1,2,3,4,5,6,7,8,9,A,B,D,E,F,G,...

What would 1AB9 mean in base 10? Well use the ((( 1*10 + A)*10 + B)*10 + 9) or ((( 1*10 + 10)*10 + 11)*10 + 9)

What properties of CM. The magnitude of CM is > 1 for 'conventional' base > 1 numbers.

What properties of CM. The magnitude of CM is = 1 for base 1 numbers.

What properties of CM. The magnitude of CM is < 1 for base 0.1 numbers.

If you have a complex number CM of magnitude 1 and an accumulator A you can itterate

  A = A * CM

The magnitude of A will increase in magnitude of CM > 1.

Example:

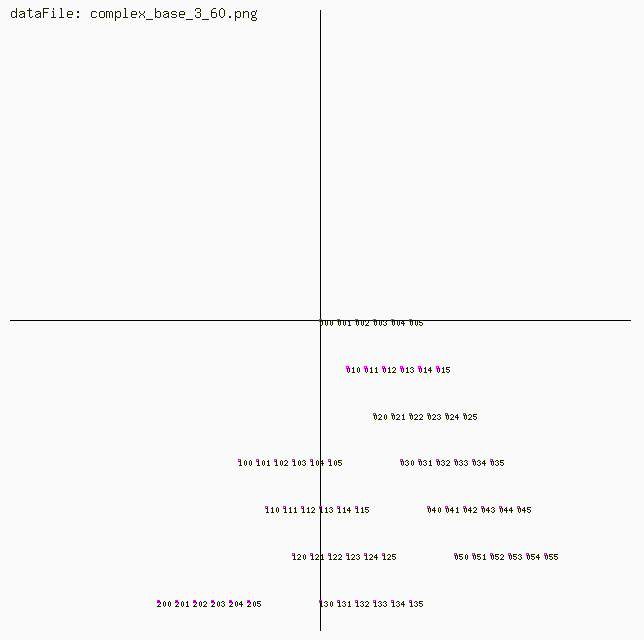
Complex Number Lines for angles 0,30,45,60,90,120 degrees for Base 6

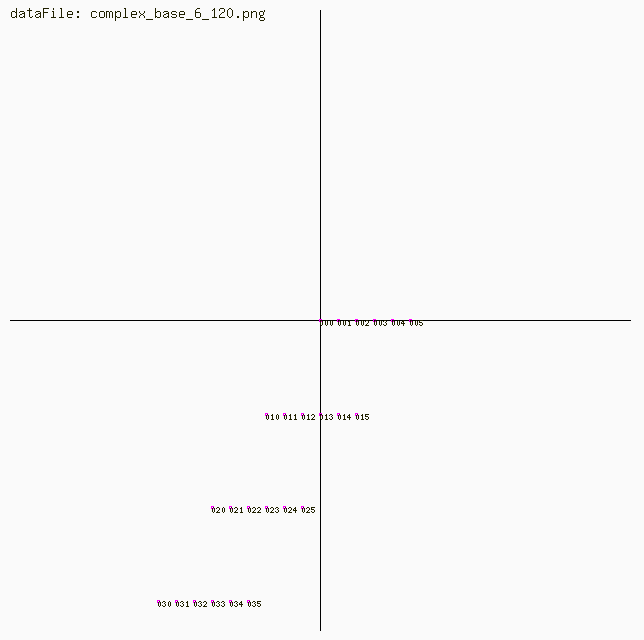
To convert 123 to symbols:

using / as integer division

   Until Number < min {
      Quotent   = Number / 10 
      Remainder = Number / 10

   Number = Quotent

   Symbol = symbolA[ int[ Remainder * 10 ] ]