“The more frequently you are able to measure and re-enforce behaviour, the faster your are able to implement change".
We live in a digital world, a world of sampled data systems.
Engineers and scientists use mathematics to describe nature, and there are certain rules that nature has to follow imposed by the laws of mathematics. Does mathematics describe nature or prescribe nature?
Most [sampled systems]? have a constant sampling rate, denoted by the black dots below.
If you apply a signal with too high a frequency, the red signal, it is aliased to the blue signal.
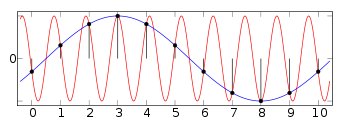see: http://en.wikipedia.org/wiki/Aliasing
If you feed me information faster than the rate I flit between jobs, I will alias some of the information.
A microprocessor only has a finite number of cycles to share out to the processes being served.
I only have a finite capacity to swap and flit between jobs. Is this a sampled data systems, with a non regular sampling frequency.
I have a finite capacity to track change and I do not read all the communications. Will I alias the message and make it go backwards if I read a sub sample of the communications?
Will I alias if I only understand a proportion of a communication?
I only understand part of the communication, and lag behind the message.
A sampled data system wraps frequency space into a circle.
Most Sampled data systems use a low pass filter to remove frequencies above half the sampling frequency. see http://en.wikipedia.org/wiki/Nyquist%E2%80%93Shannon_sampling_theorem
I may only sample some threads of information with a very limited sampling rate. If the updates to the threads of information are faster than my sampling rate, then it may appear that the information goes backwards.
A group of people may each have their own sampling rate and information changing too fast may be aliased differently by diferent people.
Sample input, take x% of input, keep 100%-x% of existing position and add x% of input.
Keeping the old, and embracing the new.
What will happen to the message if it changes faster than the rate of dissemination?
By the time I get the message it has changed.
By the time I have understood it, it has changed.
If I get overloaded, I can spend less time on understanding and accepting the change.
This is similar to the switched capacitor filter that sampled the input and uses a switch capacitor to simulate a resistor.
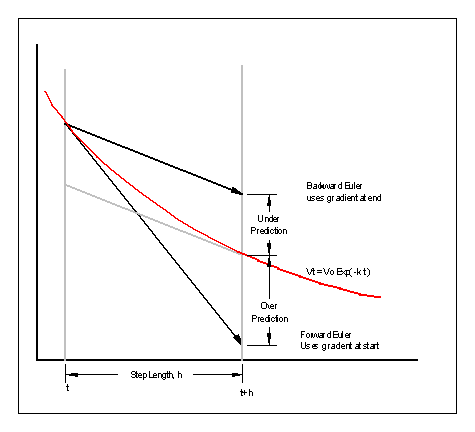
Work out the future based on how the system is changing. You assume that the rate of change will continue and use it to say how much will change in the next period. You can therefore predict where the state of the system will be at the end of the period. An alternative approach is to use the state of the system at the end of the period, and use this to steer the course of the system.
It is possible to reduce some dynamic systems to a set of first order differential equations.
Forward Euler integration is unstable if h is too large. X' is dX/dt:
X( n+1) = X(n) + X'(n)*h
Backward Euler integration is stable if h is large X' is dX/dt, X( n ) is nth point, X(n+1) is next point.
X( n+1) = X(n) + X'(n+1)*h
Normally h is a fixed time step. It would be possible to make it variable.
It may seem difficult to know the gradient of where you are going to get to, but if the system is linear, it is possible.
Let us take the simple RC network where a charged capacitor is discharged by a parallel resistor.
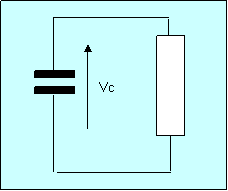
What is the voltage across the Capacitor with time?
Vr =Vc
Ic = -Ib
dVc/dt = Ic/C
Ir = Vr/R = Vc/R
dVc/dt = -Vc/RC
So we can write:
timeStep, or h, is the time we move the solution on by. Convention h is used for the time step.
Vc_now is the voltage across the capacitor now.
next_Vc is the next voltage across the capacitor after our next calculation.
Vc is the voltage across the capacitor, pick either Vc_now or next_Vc.
dVc/dt is the gradient of Vc.
next_Vc = Vc_now + timeStep * dVc/ dt
next_Vc = Vc_now - timeStep * Vc/RC
An interactive version is at http://www.dougrice.plus.com/reportCsv_files/rc.html
next_Vc = Vc_now + timeStep * dVc_now/ dt
next_Vc = Vc_now - timeStep * Vc_now/RC
next_Vc = Vc_now( 1 - timeStep */RC )
As long as timeStep << RC then this is stable.
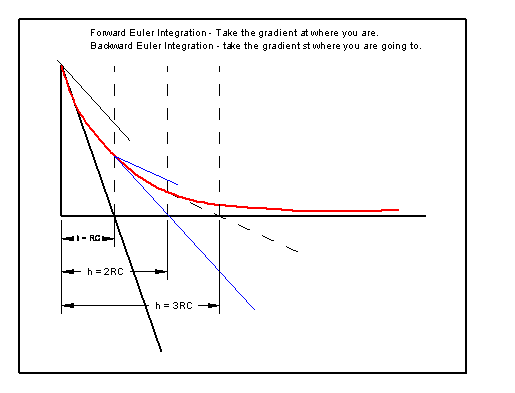
When timeStep >> RC then next_Vc may be negative, which we know from a discharging capacitor does not happen.
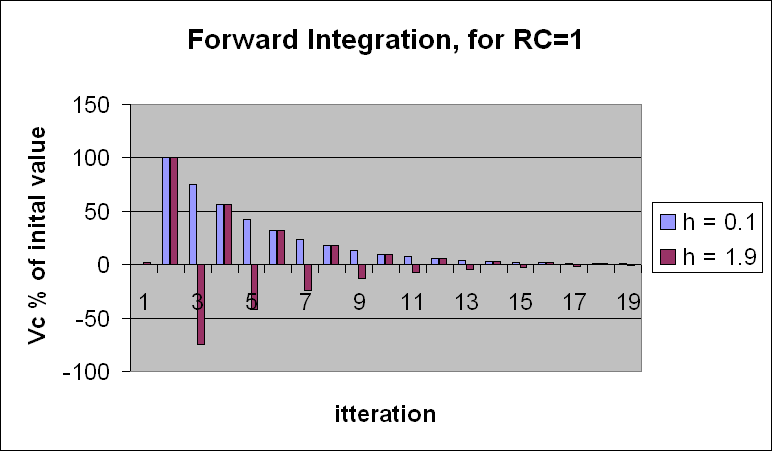
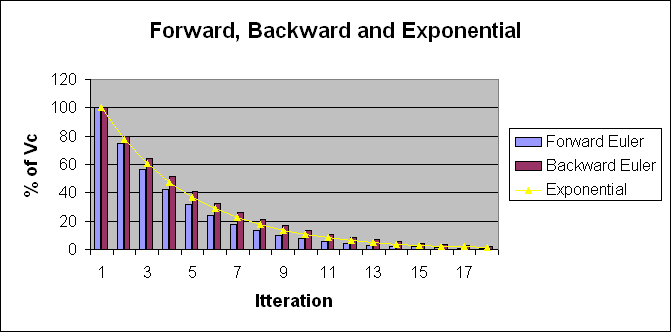
The graph is interesting, the over all decay is the same, however when timestep > RC it oscillates.
The graph is for h and ( 2 - timestep/RC ). Is this a way of finding unknown values of RC?
[exploring h]?
When timeStep/RC >> 2, then next_Vc increases in magnitude instead of decaying. The equations blow up.
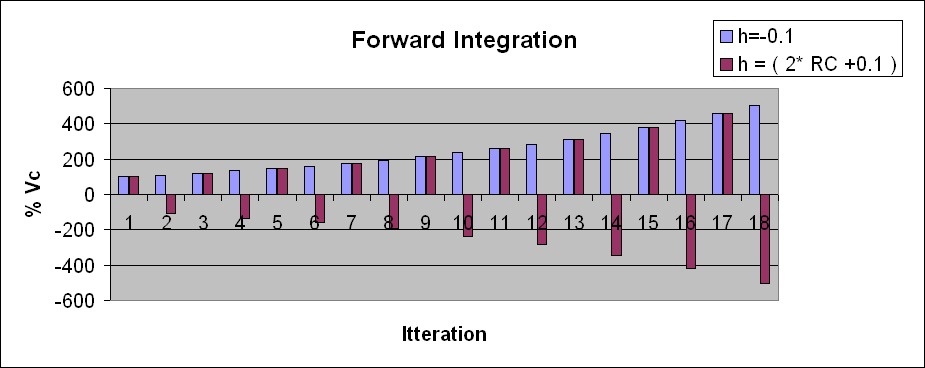
It is noted that for the simple RC first order differential equation, if you use timestep h, you get a decay, if you use a timestep of 2*RC-h you get a similar envelope, with an oscillation, every other iteration. Is this a possible way to find the Eigen values which are the time constants of the system?
The books say that to find the time constants of the matrix of first order differential equations you need to find the Eigen values. Other sources say that for large systems, the Eigen values are almost impossible to find!
http://en.wikipedia.org/wiki/Eigenvalue,_eigenvector_and_eigenspace
I was told that if I use Forward Euler Integration, then h, the timestep, must be smaller than the smallest time constant in the dynamic system. Eigen Value analysis is used to find the time constants.
see: http://en.wikipedia.org/wiki/Stiff_equation
next_Vc is the value of Vc after the next iteration.
next_Vc = Vc_now + timeStep * dnext_Vc/ dt
next_Vc = Vc_now - timeStep * next_Vc/RC
next_Vc * ( 1 + timeStep /RC ) = Vc
next_Vc = Vc_now / ( 1+timeStep/RC )
As long as timeStep > 0 then this is stable.
We take the gradient where we are and predict forward. We go to the predicted position. What happens if we work out the gradient at the new position and predict forward and also back track.
We work out the new position for timestep, h and also the position we have come from by using -timeStep and -h.
We back track we can see what error we have introduced.
This section contains Random thoughts and brain storms.
The equations above assume that the required change of direction is fully implemented. What happens when the direction is not changed to take account of the new current position? The change in gradient is not dynamic enough.
Apply Exponential smoothing to the gradient change. I am told to change to a new direction. I only change by say 50% of that required.
I am told to change to a new direction. I miss understand what is required and I undershoot or over shoot the required change.
“The more frequently you are able to measure and re-enforce behaviour, the faster your are able to implement change".
This is true. This web page explains what happens if the change is not tracked fast enough and people are set in a direction without update. This will lengthen the time step length.
If you do not correct to account for updates and changes, or conversely, the people do not take on board the changes rapidly enough, because they are getting on with other work, the system could blow up and become unstable.
If you predict the future using the direction you are currently going in, and saying that you will be there at the end of the next interval, if your direction is too agile, and subject to change, and you take too long a view of the future, the future will blow up.
It is not the dullards that cause the explosion; it is the responsive, agile bright one thing that eventually causes the chaos!
[other thoughts]?
![[Home]](../ipstats.gif)